协同过滤(CF)的一些小笔记

协同过滤(CF)的一些小笔记
DiffDayCollaborative filtering

10年之前就接触了协同过滤的概念内容,但常学常新。最近因为要在Spark MLlib中浅显应用一把,发现整体的工业界做法已经进步了很多。脑中知识的框架又有更新,记录下来,利于随机存取与向外概念贩售。
术语表
显性反馈
用户明确表示对物品喜好的行为
隐性反馈
不能明确反应用户喜好的行为。在许多的现实生活中的很多场景中,我们常常只能接触到隐性的反馈。如浏览,点击,购买,喜欢,分享
两大方向
Memory-based
这个普及的很多了,基于关注的目标,又分基于用户和基于项目两大类。除非是为了交友,否则都会转向项目推荐的数据变现目的地,一个相似消费过的东西(也靠留下的人的痕迹),一个相似的人消费过的东西。
基于用户
通过用户对共同物品的“主观价值”来筛选相似用户,再互补评分高的物品,从而达到推荐物品(项目)的目的
比较直观的协同过滤,是基于用户这一种,通过“臭味相投”的线索来做。
基于项目
通过用户集体对商品集的评价,在物品的角度上去寻找相似度高的物品,达到推荐物品的效果
物品相似度的计算用上协同过滤,是基于用户的一种变体。通过查看哪些人喜欢某一特定物品,再看这些人喜欢哪些其它物品来决定物品距离(用相似度概念不贴切)。这种变体仅相当于数据结构的反转。
1 | { |
转变成
1 | { |
最终计算一个物品与物品之间距离的矩阵表格
映射现实-此反转运用在帮零售商找到清仓物品的潜在客户方面,很直观。
总结
且一般来说,用户行为有更加明显的冷启动问题,且绝大部份用户都只生产过稀疏的显性反馈记录(评价评分),对数据集的使用利用度来说,尚不及基于项目的方式(起码热门物品集,有显性反馈的可能性较大)。
基于物品的计算,就更加聚焦高效。数据积累到一定量,物品的特征定义就更加稳定,物品间的比较不会像用户间的比较那么频繁变化,无需不停计算与每样物品最相近的其它物品,也可以削峰平谷的更高效利用计算资源。
弱势
- 物品之间的相关性,随着特征维度的增加,其计算量并不是线性增加
- 在稀疏数据集上,计算结果随着增减向量维度,计算结果不稳定
Model-based
回应如上弱势,大家就想到更线性更通用的解法来做这个事情,这样模型就出场了。模型里常见的是矩阵分解。
将用户和物品的矩阵,分解为用户因子矩阵和项目因子矩阵两个矩阵的乘积(两个矩阵乘回去,期望得到一个饱满的用户评分矩阵)。什么是项目因子乘积,咱们来举几个例子图就比较容易理解了。
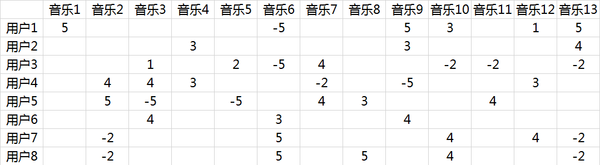
稀疏数据集
单曲循环=5, 分享=4, 收藏=3, 主动播放=2 , 听完=1, 跳过=-2 , 拉黑=-5
如上,原始用户数据集稀疏,很难相互推荐(用户本身听过的歌就不够多),现在目标就是要让数据饱满起来。
矩阵分解的数学基础是行列式变换:行变换相当于A左乘一个矩阵,矩阵A进行列变换等价于矩阵A右乘一个矩阵,因此矩阵A可以表示为$A=PEQ=PQ$(E是标准阵)
$n\times m \approx (n\times k) \times (k\times m)$
$m$ 是用户数,$n$ 是音乐数量,左侧矩阵是用户对音乐的评分,右侧是音乐在隐空间的表达和用户在隐空间的表达,二者结果尽可能逼近左侧。即由抽取的用户属性和音乐属性,尽可能还原出大型评分矩阵。这一分解通常也被称为 UV 分解
咱上面接着的例子展开,$k$ 矩阵,可以看作可量化的音乐风格因子。
用户因子
| 小清新 | 重口味 | 优雅 | 伤感 | 五月天 | |
|---|---|---|---|---|---|
| 张三 | 0.6 | 0.8 | 0.1 | 0.1 | 0.7 |
| 李四 | 0.1 | 0 | 0.9 | 0.1 | 0.2 |
| 王五 | 0.5 | 0.7 | 0.9 | 0.9 | 0 |
项目因子
| 小清新 | 重口味 | 优雅 | 伤感 | 五月天 | |
|---|---|---|---|---|---|
| 音乐A | 0.9 | 0.1 | 0.2 | 0.4 | 0 |
| 音乐B | 0.5 | 0.6 | 0.1 | 0.9 | 1 |
| 音乐C | 0.1 | 0.2 | 0.5 | 0.1 | 0 |
你可以用最大似然的办法来计算这些权重。
求权重矩阵
ALS
Alternating Least Squares - 交替最小二乘
因为两个权重矩阵都是未知的,无法直接求得,所以每次要假设一个矩阵已知,做最小二乘迭代,交替进行。(ALS是一种对目标函数进行优化的方法,通过先固定其他维度,在单独对某一维度进行更新)
SVD
Singular Value Decomposition - 奇异值分解
略
Spark内置协同过滤算法
MLlib的ALS Demo例子,这个例子排版清晰,步骤细致,做初步试验学习是最好的参照。Spark的MLlib,实现的ALS算法,已经提供了显性和隐性反馈的版本,可通过implicitPrefs =true|false(默认)来指定。
内置ALS数据集包含的行格式:电影编号,用户编号,用户电影评分,uinxtime时间戳
显隐反馈的策略区别
数据处理/看待的策略角度不同。
-
当你提供的是显性反馈时,相当于直接对你的评级数据进行建模求权重;
-
而隐式反馈时将数据集看作代表强度的数字化用户行为观察(如点击次数或某人观看项目的累积时间),这些数字与观察到的用户偏好的置信水平相关,而不是明确与评分评级有关。
当implicitPrefs = true时,还有一个配套参数 alpha(默认值1.0,也就是不干预训练结果),用来与最终模型训练结果输出前相乘。很多地方描述称做控制偏好观察中的 基线置信度,提法直观阅读比较绕,特作前面的实际作用机制说明。
补记:CTR中流行FM算法的特点
FM(Factorization Machine)是由Konstanz大学Steffen Rendle于2010年最早提出的,旨在解决稀疏数据下的特征组合问题。经过One-Hot编码之后,大部分样本数据特征是比较稀疏的,特征空间还变得更大。某些特征经过关联之后,与Label之间的相关性就会提高,那么引入特征组合就非常具有意义了。
在FM模型之前,CTR预估最常用的模型是SVM和LR(包括用GBDT给它们提取非线性特征),SVM和LR都是线性模型(SVM理论上可以引入核函数从而引入非线性,但由于非常高维的稀疏特征向量使得它很容易过拟合,故实际运用起来不太顺手),在特征关联领域,怎么建模二阶,三阶甚至更高阶非线性的关系就是预估更加准确的关键点。
因为其实际上确有相关性
- 如吃饭时间食谱类App下载量比平时大: App类别和时间的二阶关系
- 年轻男性更喜欢设计类游戏: 年龄,性别,游戏类别的三阶关系
FM通过给每个特征引入一个低维稠密的隐向量来减少二阶特征交互的参数个数,同时实现信息共享,使得在非常稀疏的特征向量上的学习更加容易泛化。理论上FM可以建模二阶以上的特征交互,但是由于计算量急剧增加,实际一般只用二阶的模型。
直观上看,FM的复杂度是 $O(kn^2)$。但是,FM的二次项可以化简,其复杂度可以优化到 O(kn)。由此可见,FM可以在线性时间对新样本作出预测
FM可以模拟二阶多项式核的SVM模型,MF模型,SVD++模型等,相比SVM的二阶多项式核而言,FM在样本稀疏的情况下是有优势的。FM的训练/预测 复杂度是线性的,而二阶多项式核SVM需要计算核矩阵,核矩阵复杂度就是$\mathcal{O}(n^2)$。
参考补充
- 1.CSDN 推荐算法(一)——音乐歌单智能推荐 ↩