堆排序与归并排序

DiffDay2023-01-162024-06-18

大家最常见的就是用数组这一数据结构来记录一系列有序或无序的数据。

堆排序

Heap

此文讲的堆和堆内存不是一个概念。属于大家都形而上的用了这个英文词来描述自己的领域概念。

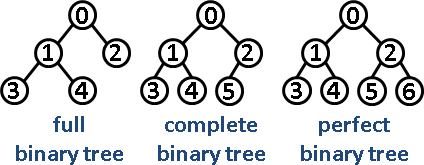
完全二叉树

叶子结点只出现在最下层和次下层（所有分支长度几乎相同，最长分支最短分支差异最多为1），最下层节点都集中在最左边若干位置的二叉树

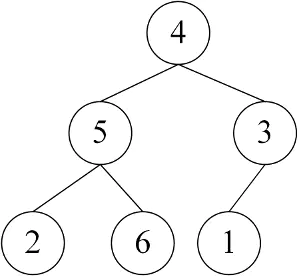
堆也是一颗完全二叉树，举例如下无序数组：$\begin{bmatrix}4 &5 &3 &2 &6 &1 \end{bmatrix}$。表示为完全二叉树的形式为

基于完全二叉树的基本性质，可从数组索引角度描述数字与数字在二叉树中的位置关系，堆的结构性要求其为完全二叉树，就为了使用此好特性好结论

$A_i$ 的左节点为 $A_{2i+1}$
右节点为$A_{2i+2}$
父节点为 $A_{i/2}$

Full vs Complete vs Perfect

二叉树通常用链表通过指针实现。堆的“(almost)-complete”属性及所有非叶子节点也是数值节点，对于将其实现为数组非常有用。堆为完全二叉树，我们可使用位置来确定哪个节点是哪个节点的子节点，i，2i+1，2i+2。

almost-complete 和 complete是一个意思

full binary tree 要求只要你有孩子，就必然是有两个孩子，但不要求所有长短分支差异最多为1的约束，也不要求孩子在最左边位置优先集中

堆序性

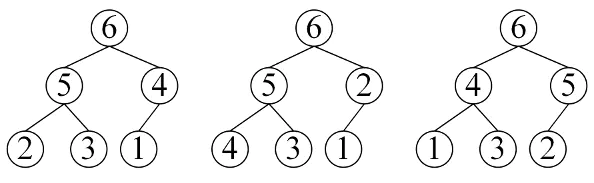
堆序性，通俗点也是说，父节点中的元素不小于（不大于）任意子节点的元素。

我们举例大根堆，一个节点元素在其子树所有元素组成的集合中必定是最大值。

如下3个，都是符合定义的大根堆

具体实现

根据无序数组创建一个大根堆，不断调整大根堆，使其达到有序。

堆排序是一种算法，可归纳为2个步骤：

将输入数组转换为堆 – 初始堆排序
将堆转换为排序数组 – 堆排序输出

交换-下沉

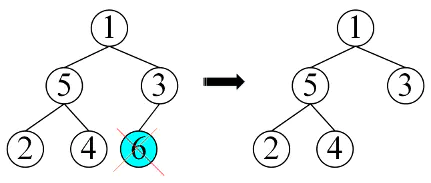
将根元素与最后一个叶子节点元素交换位置，这样做产生了两个后果：

最大值6被挑选出来，置于数组的末位（1和6换位置）【首尾交换】
根节点元素1打乱了堆序性

其中第2点不是我们希望的结果，那就重复做这个过程（此时，尾部元素6不参与任何交换位置操作，已经是最终位置，且它确定是最大值，后续的二叉树可以将元素6排除在外）【元素下沉】

每次堆顶元素与数组尾部元素互换后，我们要处理生成最大堆树的节点数据都会减一

通过重复提取最大元素，在$\mathcal{O}(n\log(n))$的复杂度下，可轻松使用它生成排序数组（提取的元素放置在数组末尾，不再参与下一轮的堆处理中）。

这一点上，大根堆实现数组从小到大排序；小根堆实现数组从大到小排序。

概念Tips

堆本身不是排序数组

原始数组

1	[9,7,3,5,4,2,0,6,8,1]

转换成堆

1	[0,1,2,5,4,9,3,6,8,7]

而排序数组是

1	[0,1,2,3,4,5,6,7,8,9]

堆看上去元素顺序看起来不像原始数组中那样随机，但它们没有完全排序。

堆形式并不是唯一的

对于给定的无序数组，根据算法的叶子节点左右大小设定不同，可以构建出多个大根堆，即可以生成的大根堆并不是唯一的

上段中的数组，转换成堆不止一种形式

       0
      /      \
     1        2 （这里2，1左右互换，也是符合堆的含义的）
   /   \     / \
  5     4   9   3
 / \   / \ / \ / \
6   8 7

归并排序

兄弟排序算法

冒泡排序和选择排序，是最好理解最容易实现的两种排序算法。

冒泡：交换相邻两个元素，将最大元素升至最后位置（像水中的冒泡）
选择：遍历所有元素，选出最小的，放在排序序列头部，然后再从未排序元素中继续寻找最小的，放到已排序序列末位，以此类推直至排好所有元素（这点的一个个来，和堆排序有那么一点神似）

这二位相较于其他排序算法，除了易于理解外，并无任何优势，所以在实际开发或类库中，基本没人用。

插入排序，像打扑克牌，核心是将某个元素插到合适位置，该元素后所有元素都后移一个位置（比较和挪动到抽牌处为止）。适用场景为大部分数据近乎有序。如原始数据根据订单完成时间排序，现需要根据订单发起时间排序，这样每个元素就能很快挪到正确位置。这个动图比较形象插入排序动图
快速排序是最快的的通用排序算法，多数情况下，都适合适用快速排序。

外部排序的选择

归并排序：将已排好序的两部分进行归并（合在一起），动图的话观看归并排序动图

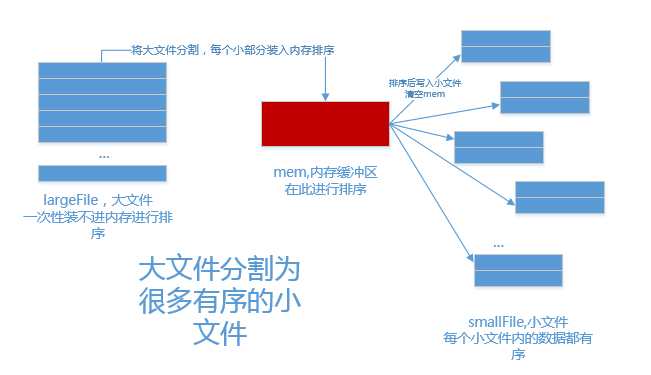
当待排序的文件超过内存可使用容量，文件无法一次性放到内存中进行排序，需要借助外部存储器，称为外部排序。外部排序算法由两个阶段构成，类比为Map-Reduce过程也合适

按内存大小，将大文件分成若干子文件，将各子文件依次读入内存，适用恰当的内部排序算法对其进行排序，将排好序的归并段重新写入外存，为下一个子文件排序腾出内存空间
对得到的顺序段进行合并，直至得到整个有序文件位置。

例如含有1w个记录的文件，内存可使用容量仅为1k个记录，毫无疑问需要使用外部排序算法（可以看作是选择排序的组合版）。

实际归并过程中，由于内存容量限制不能满足同时将2个归并段全部完整的读入内存进行归并，只能不断取2个归并段中的每一小部分进行归并，通过不断读取数据和向外写数据，直至2个归并段完成归并成1个大的有序文件。

多路归并

堆外部排序算法来说，影响整体排序效率的因素主要为读写外存的次数，即访问外存越多，花的时间也越多。

简单来看，访问外存的次数同归并次数成正比（每次归并都要在外存中暂存结果），两个角度可助力提高算法效率

减少初始归并段的数量m，即增加每个归并段(小文件)的容量
增加k-路同行归并的段数

因此在m个初始段下，提高归并时参与的段数，可以加快效率。这也是多路归并的由来

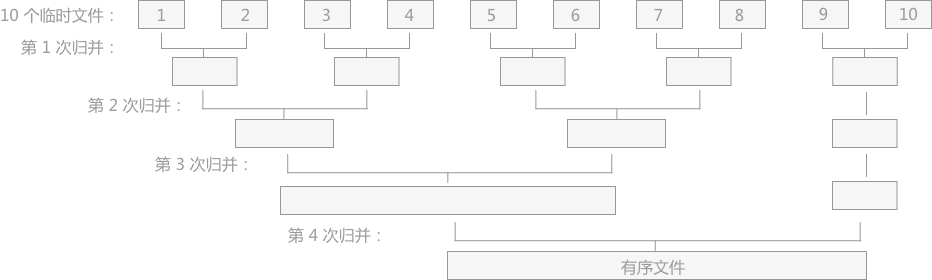
多路举例

2路归并

2路归并

5路归并

归并路数扩大的弊端

无限度增加K值，虽会减少读写外存数据的次数，但会增加内部归并的时间。

2路归并，每次从2个文件中得到一个最小值只需比一次，5路归并时要比4次。

如要得到整个临时文件，耗费的时间就会相差很大，如何同等参数下优化算法缩减比较次数（耗时）呢？

算法优化登场

结论先行

最小堆 $\Rightarrow$ 胜者树 $\longrightarrow$ 败者树

首先选择用来做外部排序优化的是最小堆，(小文件内部为最小堆)，它的插入和查询复杂度都是$\mathcal{O}(\log(n))$，可以说比较高效。不过，堆调整时，每个节点都需要和左右孩子进行比较，即需要2次比较。在不考虑块读取优化的外部排序中，也就是需要读取两次外存，能不能再优化下呢？

树排与堆排

二叉堆

二叉堆除了可以应用于对一个数组进行堆排序外，还可以应用于多路归并排序中。

堆排序的后半部分算法中，就是一个很明确的，多个值中选取极值，取出极值，更新根，然后修复堆的过程。在多路归并排序中，每次取出极值后，堆长度未变

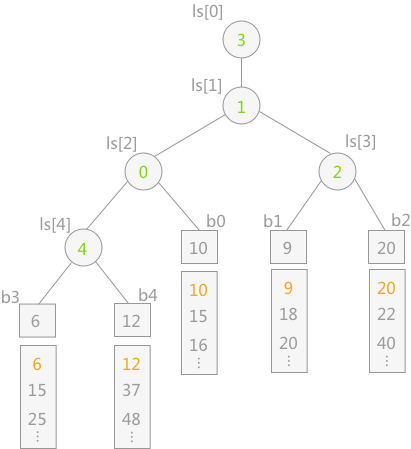
胜者树

树排，全称可叫树形选择排序，因为其排序过程和体育比赛中的8进4, 4进2, 2争冠非常相似，所以树排又称为锦标赛排序，且树排中用到的树就是胜者树（8进4，4进2，2争冠嘛）

树排算法很简单：

建树。注意事项是胜者树种的节点都是原数组中的索引，而不是真实值（因为第二步要拿到冠军的索引，节点都在叶子上），然后一路向上更新胜者树
冠军出堆，然后找到冠军的索引，将此索引处的值变成inf（要求最小），进行siftUp调整，剩余元素个数-1

重复上述步骤直至剩余元素个数为0，此时按照出堆顺序就是从小到大的。

胜者树的特征

1
2
3

1. 完全二叉树 
2. 每个叶子节点表示一个选手，记录选手的标号
3. 每个非叶子节点表示一场比赛，记录胜者（数值小的）的标号，每层表示一轮比赛

胜者树

新插入选手（红色–来自另一个归并段的胜者），胜者树重构

胜者树重构

胜者树与堆的异同

都是完全树，时间复杂度量级也一样，最大的区别就是堆的非叶子节点有包含元素，而胜者树只有叶子节点有元素，非叶子节点用来存放两个节点的胜者。由于此结构上的差异，在每次调整的时候堆分别要跟两个孩子进行两次比较，而胜者树只需要跟兄弟进行一次比较即可，效率上会高一点（路径保存了额外的信息）。

树深度的疑问

但大家可能有疑问，你比较次数虽然少了，但堆非叶子节点也含有原始数据，所以堆的树高度会比胜者树低，那么要调整的次数少了，综合起来是否差不多？

请注意，大家都是完全二叉树，每增加一层，节点数目可容纳就多了一倍，因此堆的高度一般也之比胜者树矮一层，这样定性来分析，堆在高度上也只有很小的优势。

胜者树vs败者树

胜者树在内部排序有用，而败者树在外部排序的多路平衡归并中有用武之地，怎么讲？其实现在程序的主要瓶颈在于访存了，计算倒几乎可以忽略不计了，谁能在减少比较/更新次数上更胜一筹，谁将拔得头筹！这必然要重新调整数据结构设计

比较胜者树与败者树的代码，非常相似，都像是一根根不断将数组中的水（数组元素）吸取上来然后吐出来，也都是完全二叉树，是树形选择排序的一种变形。

胜者树，新元素上升时，首先需获得父节点值（内容是下标），然后再获得兄弟节点的值进行比较，相较于堆减少了一半的比较量。且因为新插入的值取代了原先的最优胜者，新值向上调整的过程中，必然要更新父节点，能不能再优化呢？

败者树就抓住者一小点再做优化

胜者树种的非叶子节点存储的是胜利的一方；而败者树非叶子节点存储的是失败的一方，而在比较过程中，都是拿胜者去比较。有一个额外指针保存当前的胜者。

败者树解决了胜者树存在的弊端，只需和父节点比较一次，新插入的值向上调整中，不一定要更新【总得来说，减少了访存时间】。

胜者树和败者树在每输出和补充一个值之后都需要自底向上调整，每上升一层都需要一次比较，败者树是和父节点的一次比较，胜者树适合兄弟的一次比较，在比较的内存次数上二者没有太大的差别。不同的是胜者树每次必然需要更新胜者（这条路径就是以原来的最终胜者为外部节点的路径，而原来的最终胜者已经被输出了），但败者树每次不一定需要更新，这代表它在每次上升时可能会少一次向内存的写入，因此更优。

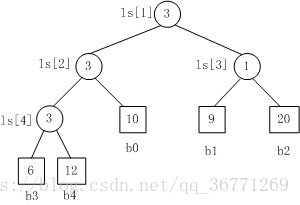
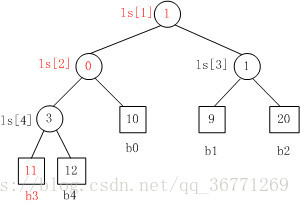
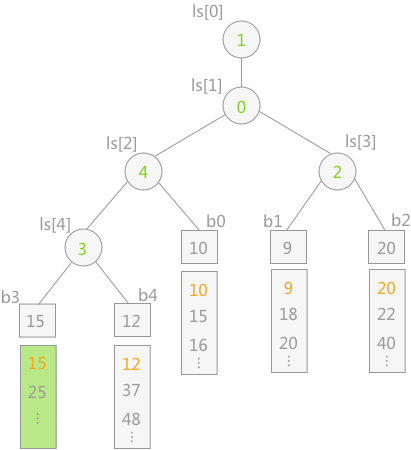
败者树工作过程

5路归并败者树

如上图为一个5路归并的败者树，其中b0 ~ b4为叶子节点，分别为5个归并段中存储的记录的关键字。ls位一维数组，表示非叶子节点，存储的数值表示第几归并段（如b0就为第0归并段），ls[0]中存储的为最终胜利者，如图表示第3归并段中的值最小。

当胜利者筛选出来后，只需要更新叶子结点b3的值，即导入15，然后让该节点不断与其父亲节点表示的值进行比较，败者留在父亲节点，胜利者继续向上比较

败者树的工作过程

为防止归并过程中某个归并段变空，处理办法通常是在每个归并段最后附件一个关键字为最大值的记录，这样当某一时刻选出冠军位为最大值时，表明所有归并段已全部归并完成。

量化对比

在堆，胜者树，败者树，空间和时间复杂度都一样，没有量级上的差别，但还是有优中选优的差异。

堆不消多说，胜者树每次从k个组中首元素中选一个最小的值，加入到新组，都要比较k-1次，算法复杂度就是 $\mathcal{O}((n-1)(k-1))$，而如果用败者树，可以在$\mathcal{O}((n-1)\log(k)$的复杂度下，得到最小的数。对于外部排序这种数据量超大的排序来说，也是一个不小的提高，故外部排序大多采用的都是败者树算法实现的【在信息爆炸的年代，海量数据大文件排序是很普遍的】。

外排序本质上在真正排序的时候用的还是内排序的算法，毕竟CPU不能直接和外存打交道。外部排序比内排序在同等算法下要慢得多，根本原因在于IO时间相比内存和cpu交互运算时间太长，所以外部排序的算法主要集中的地方在于如何有效降低读写外存的次数，次数越多，算法效率越低，一种思路就是增加k路平衡归并中的k值。但无限增加k值，虽会减少读写外存的次数，但会增加内部归并的时间。败者树数据结构使得在增加 K 值时不会线性的影响内部归并的效率，所以成为一种优中之选。